VRChat Vector Mathematics

Ways to calculate vector with GameObject transform and VRC_SceneResetPosition.

Object transform and VRC_SceneResetPosition are vector math library in VRChat!

Notation

• For any vectors : A, B
• For local space origin : O
• For rotation matrix : r
• For scalar : k
• For indexing local space :
  • _ps: in problem space
  • _ss: in solution space

Object hierarchy :

P        // local root
 - Q     // child object
    - R  // grand child object

Move vector

Move a vector to another local space. A_ps => A_ss

implementation:

1. Move P to O_ps
2. Move Q to A_ps
3. Move P to O_ss
4. Then, Q is at A_ss

Add vectors

Add two vectors in problem space and get result in solution space. ( A_ps, B_ps ) => (A + B)_ss

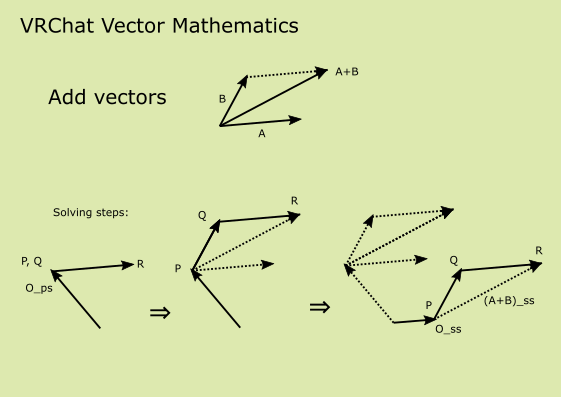
implementation:

1. Move P and Q to O_ps
2. Move R to A_ps
3. Move Q to B_ps
4. Move P to O_ss (skippable if O_ps = O_ss)
5. Then, R is at (A + B)_ss

Subtract vectors

Subtract two vectors in problem space and get result in solution space. ( A_ps, B_ps ) => (A - B)_ss

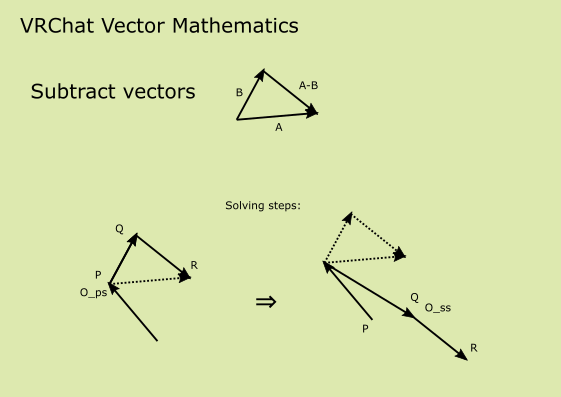
implementation:

1. Move P to O_ps
2. Move Q to B_ps
3. Move R to A_ps (R's local transform is subtract result)
4. Move Q to O_ss
5. Then, R is at (A - B)_ss

Rotate and scalar multiplication

Rotate a vectors in problem space and get result in solution space. Scalar multiplication solution is identical. So both could be done at once.

• ( r_ps, A_ps ) => (r * A)_ss
• ( k, A_ps ) => (k * A)_ss
• ( k, r_ps, A_ps ) => (k * r * A)_ss

implementation:

1. Move P and Q to O_ps
2. Move R to A_ps
3. Move Q to r_ps
4. Move P to O_ss
5. Then, R is at (r * A)_ss

Acknowledgments

I lean this technique from http://vrchat.wikidot.com/worlds:guides:player-tracking by CyanLaser. Thank you for sharing your wonderful work.